[알고리즘] 분할정복 방법 - 이진 탐색, 퀵 정렬 알고리즘
1. 분할정복(Divide-and-Conquer) 방법
- 대표적인 알고리즘 설계 기법 중 하나
- 대표적인 알고리즘 설계 기법 : 분할정복(divide-and-conquer) 방법, 동적 프로그래밍(dynamic programming) 방법, 욕심쟁이(greedy) 방법
1) 분할정복 방법의 원리
- 순환적(recursive)으로 문제를 푸는 하향식(top-down) 접근 방법
주어진 문제의 입력을 더 이상 나눌 수 없을 때까지 순환적으로 분할하고 분할된 작은 문제들을 해결한 후 그 해를 결합하여 원래 문제의 해를 구하는 방식
2) 분할정복 방법의 특징
- 분할된 작은 문제는 원래 문제와 성격이 동일하다. → 입력 크기만 작아짐
- 분할된 문제는 서로 독립적이다. → 순환적 분할 및 결과 결합 가능
3) 분할정복 방법의 처리 과정 : 분할 → 정복 → 결합
분할정복 방법의 각 순환 호출 시의 처리 과정
- 분할 : 주어진 문제를 여러 개의 작은 문제로 분할
- 정복 : 작은 문제들을 순환적으로 분할하고 작은 문제가 더 이상 분할되지 않을 정도로 크기가 충분히 작다면 순환호출 없이 작은 문제에 대한 해를 구함
- 결합 : 작은 문제에 대해 정복된 해를 결합하여 원래 문제의 해를 구함
4) 분할정복 알고리즘 - 이진 탐색, 합병 정렬, 퀵 정렬, 선택 문제
분할정복 방법이 적용된 이진 탐색, 합병 정렬, 퀵 정렬, 선택 문제 알고리즘에서의 분할 과정

- n은 입력 크기 = 데이터 수를 의미
- 검정색으로 표시된 부분은 문제에서 배제된 부분
- 이진 탐색과 합병 정렬은 일정하게 절반씩 분할
- 퀵 정렬과 선택 문제는 분할 크기가 일정하지 않음
2. 이진 탐색(Binary Search)
* 정렬된 데이터에 대한 효과적인 탐색 방법 (오름차순으로 정렬되었다고 가정)
* 입력이 정렬된 리스트에 대해서만 적용 가능
* 삽입/삭제 연산 시 데이터의 정렬 상태 유지 필요
- 평균 n/2개의 데이터 이동 발생
- 삽입/삭제가 빈번한 응용에 부적합
* 배열의 가운데 원소와 탐색키 x를 비교
1) 탐색키 = 가운데 원소 → 탐색 성공
2) 탐색키 < 가운데 원소 → '이진 탐색(크기 ½의 왼쪽 부분배열)' 순환 호출
3) 탐색키 > 가운데 원소 → '이진 탐색(크기 ½의 오른쪽 부분배열)' 순환 호출
* 탐색을 반복할 때마다 대상 원소의 개수가 ½씩 감소
* 성능 : Θ(logn)
1) 이진 탐색의 분할정복 과정
- 분할 : 배열의 가운데 원소를 기준으로 왼쪽, 오른쪽 부분배열로 분할. 탐색키와 가운데 원소가 같으면 반환 및 종료
- 정복 : 탐색키가 가운데 원소보다 작으면 왼쪽 부분배열을 대상으로 이진 탐색을 순환 호출, 크면 오른쪽 부분배열을 대상으로 이진 탐색을 순환호출
- 결합 : 탐색 결과가 직접 반환되므로 결합 불필요
2) 이진 탐색 알고리즘 - 순환 형태
BinarySearch(A[], Left, Right, x) {
if (Left > Right) return -1; // 탐색 실패
Mid = floor((Left + Right)/2); // 바닥 함수
if (x == A[Mid]) return Mid;
else {
if (x < Mid) BinarySearch(A, Left, Mid-1, x); // 왼쪽 부분배열
else BinarySearch(A, Mid+1, Right, x); // 오른쪽 부분배열
}
}
3) 이진 탐색 알고리즘 - 반복 형태
BinarySearch_Iteration(A[], n, x) {
Left = 0;
Right = n-1;
while (Left <= Right) {
Mid = floor((Left+Right)/2); // 바닥 함수
if (x == A[Mid]) return Mid; // 탐색 성공
else {
if (x < Mid) Right = Mid - 1; // 왼쪽 부분배열
else Left = Mid + 1; // 오른쪽 부분배열
}
return -1; // 탐색 실패
}
4) 이진 탐색의 성능
- T(n) = logn
(1) 입력 크기가 n일때 최대 분할 횟수 k
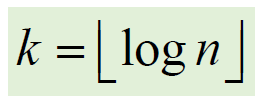
예) 입력 크기 n = 8이면 최대 분할 횟수 k = 3
(2) 입력 크기가 n일때 최대 비교 횟수
최대 분할 횟수 + 1
(3) 성능
BinarySearch(A[], Left, Right, x) {
// 중략..
if (x == A[Mid]) return Mid; // 바깥 수준
else {
// 순환 호출
if (x < Mid) BinarySearch(A, Left, Mid-1, x);
else BinarySearch(A, Mid+1, Right, x);
}
}T(n)
= 입력 크기 n에 대한 탐색 과정에서의 모든 비교 횟수의 합
= 바깥 수준에서의 비교 횟수 + 순환 호출에서의 비교 횟수

3. 퀵 정렬(Quicksort)
* 특정 원소 피벗(pivot)을 기준으로 주어진 배열을 두 부분배열로 분할하고 각 부분배열에 대해 퀵 정렬을 순환적으로 적용하는 방식

분할 후 왼쪽 부분배열의 모든 값 < 피벗 < 오른쪽 부분배열의 모든 값
* 최선/평균 성능 Θ(nlogn)
* 최악 성능 Θ(n²)
* 최악의 경우가 발생할 가능성은 거의 없음
- 피벗 선택의 임의성이 보장되면 평균적인 성능을 보일 가능성이 매우 높음
- 배열에서 임의로 값을 선택해서 배열의 처음 원소와 교환 후 정렬 수행
1) 퀵 정렬의 분할정복 과정
- 분할 : 피벗을 기준으로 배열을 두 부분배열로 분할
- 정복 : 두 부분배열에 대해 퀵 정렬을 순환적으로 적용하여 각 부분배열을 정렬
- 결합 : 결합 불필요
2) 퀵 정렬 알고리즘
void QuickSort(A[], n) {
if (n>1) {
pivot = Partition(A[0...n-1], n); // 두 부분배열로 분할
QuickSort(A[0...pivot-1], pivot); // 왼쪽 부분배열 순환 호출
QuickSort(A[pivot+1...n-1], n-pivot-1); //오른쪽 부분배열 순환 호출
}
}
int Partition(A[], n) {
Left = 1;
Right = n-1;
while (Left < Right) { // 피벗 A[0]
// 피벗보다 큰 값의 위치를 찾음
while (Left < n && A[Left] < A[0]) Left++;
// 피벗보다 작은 값의 위치를 찾음
while (Right > 0 && A[Right] >= A[0]) Right--;
// Left, Right 교환
if (Left < Right) exchange(A[Left], A[Right]);
// 피벗, Right 교환
else exchange(A[0], A[Right]);
}
}

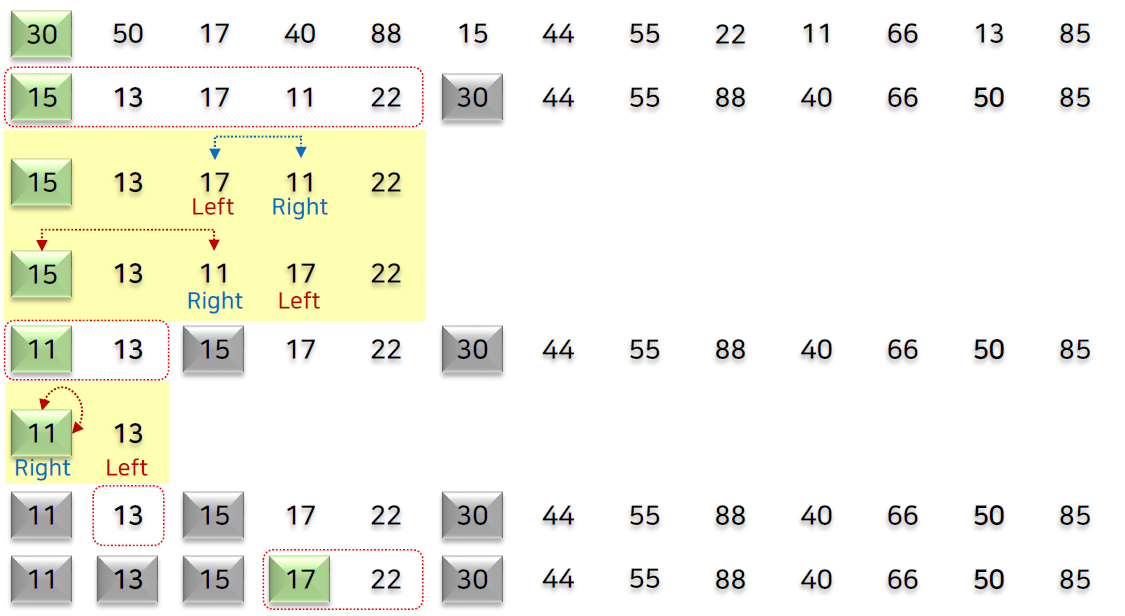
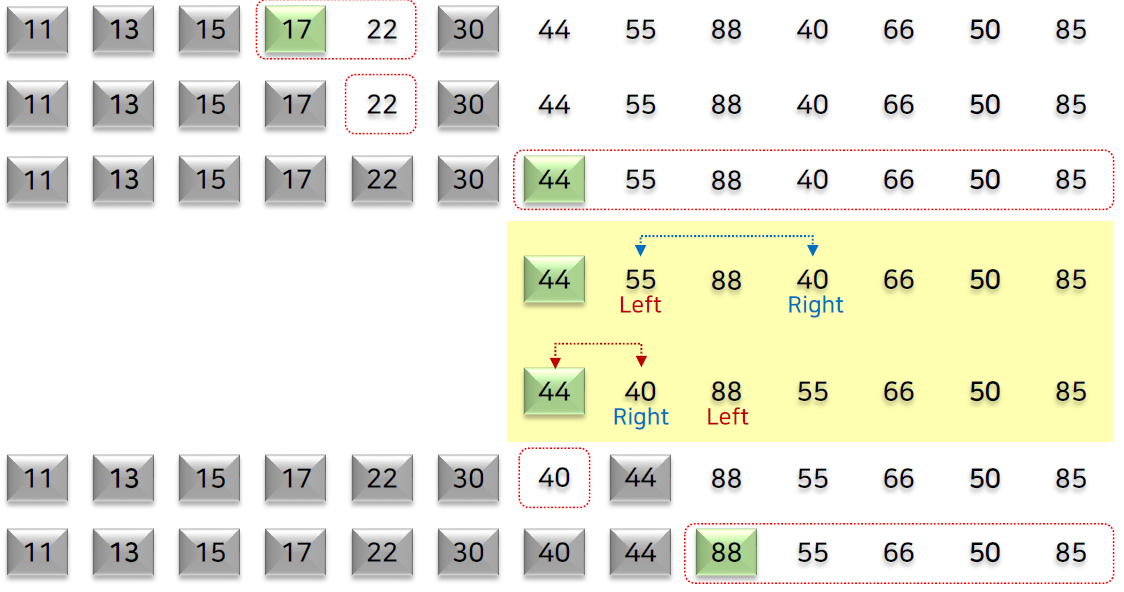

3) 퀵 정렬의 성능
- 평균 : T(n) = O(nlogn)
- 최악 : T(n) = O(n²)
- 최선 : T(n) = O(nlogn)
(1) 분할 함수 Partition()의 수행 시간
Θ(n)
퀵 정렬의 분할 함수는 Θ(n)의 선형 시간을 갖는다.
(2) 퀵 정렬 QuickSort() 수행 시간 분석
T(n)
= 한 번의 분할 함수 Partition() 호출 + 두 번의 퀵 정렬 함수 QuickSort() 호출
= Θ(n) + 두 번의 퀵 정렬 함수 QuickSort() 호출
* 퀵 정렬 - 최악의 경우

- 피벗을 제외한 나머지 모든 원소가 하나의 부분배열로 분할되는 경우 : 즉 피벗이 항상 부분배열의 최소값 혹은 최대값이 되는 경우
- 입력 데이터가 정렬된 데이터이고 피벗이 배열의 처음 원소인 경우

* 퀵 정렬 - 최선의 경우

- 피벗을 중심으로 항상 동일한 크기의 두 부분배열로 분할되는 경우
- 피벗이 항상 부분배열의 중간값이 되는 경우

References
'Computer Science' 카테고리의 다른 글
| 소프트웨어 개발 프로세스 모델 - 폭포수 모델(Waterfall Model) (0) | 2020.04.18 |
|---|---|
| [컴퓨터보안] 암호의 개념과 대칭키 암호, 공개키 암호 (0) | 2020.04.05 |
| [컴퓨터보안] 정보보호의 목표 - 기밀성, 무결성, 가용성 (0) | 2020.03.23 |
| [컴퓨터공학/소프트웨어공학] 소프트웨어 공학 개요 (0) | 2020.03.22 |
| [알고리즘] 알고리즘의 설계와 분석 - 시간 복잡도와 점근성능 (0) | 2020.03.11 |




댓글